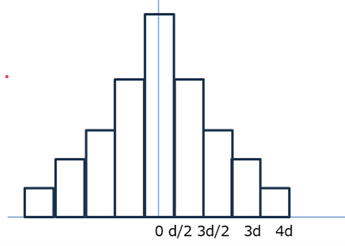
・正規分布
次は,化学反応ではなく正規分布の場合,これも累積関数でフィットできます.
正規分布の確率分布は,
\(\Large \displaystyle P(x) = \frac{1}{\sqrt{2 \pi } \sigma } exp \left[- \frac{ (x - \mu)^2}{2 \sigma^2} \right] \)
ですが,ピークの高さを求めるので,平均値,μ,は無視してかまいません.
\(\Large \displaystyle P(x) = \frac{1}{\sqrt{2 \pi } \sigma } exp \left[- \frac{ x ^2}{2 \sigma^2} \right] \)

ですので,0~d/2,まで積分して2倍した値がその割合となります.
\(\Large \displaystyle 2 N \int_0^{d/2} \frac{1}{\sqrt{2 \pi } \sigma } exp \left[- \frac{ x ^2}{2 \sigma^2} \right] dx \)
ここで,
\(\Large \displaystyle \frac{ x ^2}{2 \sigma^2} \equiv y^2 \)
とすれば,
\(\Large \displaystyle \frac{ x }{\sqrt{2} \sigma} = y \)
\(\Large \displaystyle \frac{ dx }{\sqrt{2} \sigma} = dy \)
x,yの範囲は,
\(\Large \displaystyle 0 \hspace{20 pt} < \hspace{20 pt} x \hspace{20 pt} < \hspace{20 pt} d/2 \)
\(\Large \displaystyle 0 \hspace{20 pt} < \hspace{20 pt} y \hspace{20 pt} < \hspace{20 pt} \frac{d}{2 \sqrt{2} \sigma} \)
となるので,
\(\Large \displaystyle 2 N \frac{1}{\sqrt{2 \pi } \sigma } \int_0^{\frac{d}{2 \sqrt{2} \sigma}} exp (- y^2 ) \ \sqrt{2} \sigma \ dy \)
\(\Large \displaystyle = \frac{2N}{\sqrt{ \pi }} \int_0^{\frac{d}{2 \sqrt{2} \sigma}} exp (- y^2 ) \ dy \)
となります.この積分は,誤差関数で表すことができます.誤差関数は,
\(\Large \displaystyle erf(x) = \frac{2}{\sqrt{ \pi }} \int_0^{x} exp (- t^2 ) \ dt \)
ですので,
\(\Large \displaystyle = \frac{2N}{\sqrt{ \pi }} \int_0^{\frac{d}{2 \sqrt{2} \sigma}} exp (- y^2 ) \ dy \)
\(\Large \displaystyle = 2 N \frac{1}{\sqrt{ \pi }} \frac{ \sqrt{ \pi}}{2} erf \left( \frac{d}{2 \sqrt{2} \sigma} \right) \)
\(\Large \displaystyle = N \cdot erf \left( \frac{d}{2 \sqrt{2} \sigma} \right) \)
とピークの値を表すことができます.
・実際の計算
実際に,正規分布を作成して(=NORMINV(RAND(),mean,sd)),mean,sdを色々変えて計算させると,
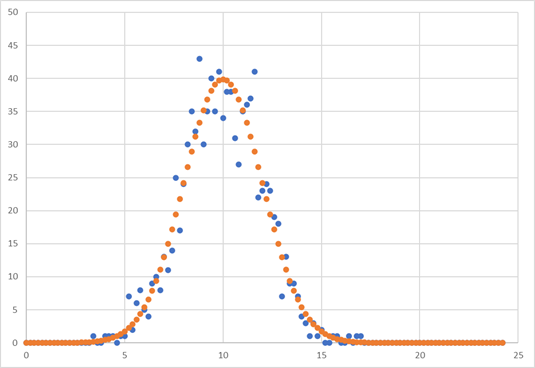
μ=10, σ=2, d=0.2, N=1000, -> Peak=39.88
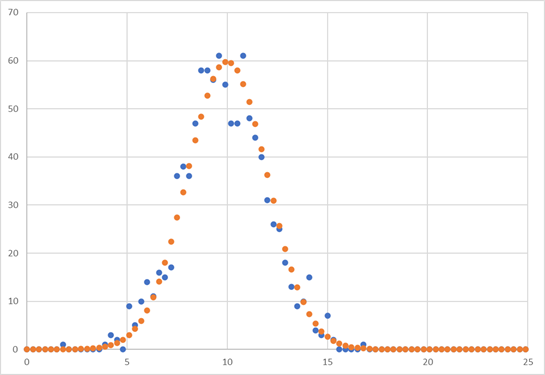
μ=10, σ=2, d=0.3, N=1000, -> Peak=59.79
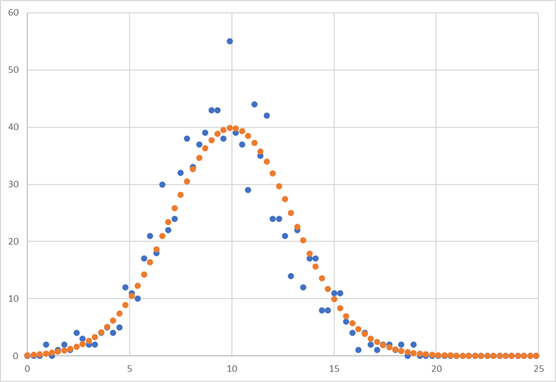
μ=10, σ=3, d=0.3, N=1000, -> Peak=39.88
ときれいにフィットできました.